O ciclo diesel teórico é um modelo termodinâmico que descreve o funcionamento ideal de motores diesel, amplamente utilizados em veículos de transporte, geradores de energia e máquinas industriais.
Este ciclo é uma abordagem teórica que permite analisar o desempenho do motor através do estudo das transformações físicas e químicas pelas quais o combustível passa ao longo do processo.
Como a análise de um ciclo real envolve um grande número de variáveis e fatores complexos, são utilizados modelos simplificados baseados em certas suposições teóricas. Essas aproximações permitem estudar sua eficiência e comportamento sem ter que considerar todas as perdas e efeitos colaterais presentes em um motor real.
Fases do ciclo diesel ideal
O ciclo diesel consiste em quatro estágios principais: admissão, compressão, combustão e exaustão. Cada um deles é explicado em detalhes abaixo:
1. Admisión
Nesta fase, o pistão está no topo de seu curso. As válvulas de admissão abrem e permitem que o ar entre no cilindro à pressão atmosférica.
Ao contrário dos motores a gasolina, onde é introduzida uma mistura de ar e combustível, os motores a diesel introduzem apenas ar.
2. Compressão
O pistão sobe e comprime o ar no cilindro, reduzindo seu volume e aumentando significativamente sua pressão e temperatura.
Esse aumento de temperatura é crucial, pois prepara o ar para a combustão espontânea do diesel, sem a necessidade de faísca, de acordo com a lei dos gases.
3. Combustão e expansão
Quando o pistão atinge o topo de seu curso, o combustível diesel é injetado na câmara de combustão. Devido à alta temperatura e pressão do ar comprimido, o combustível inflama espontaneamente.
A combustão causa uma rápida expansão dos gases, gerando uma força que empurra o pistão para baixo. Esse movimento é o que converte energia térmica em trabalho mecânico, usado para movimentar o veículo ou operar um gerador.
4. Fuga
Após a expansão, o pistão sobe novamente, expelindo os gases de combustão através das válvulas de escape.
Esses gases podem ser liberados no ambiente ou passar por um sistema de filtragem para reduzir emissões e ruídos.
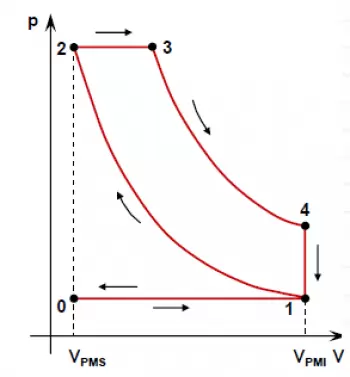
Diagrama PV do ciclo ideal do motor diesel
O ciclo teórico do motor diesel é comumente representado em um grafico chamado "Diagrama Pressão-Volume" ou "Diagrama PV".
Este diagrama mostra como a pressão e o volume dentro do cilindro do motor variam durante os quatro estágios do ciclo diesel.
Compressão adiabática (1 → 2)
- O pistão sobe e comprime o ar sem troca de calor .
- A pressão e a temperatura aumentam consideravelmente.
- No diagrama, esta fase é representada por uma curva ascendente do ponto 1 ao ponto 2.
Combustão de pressão constante (2 → 3)
- O pistão atinge seu ponto superior e o combustível é injetado.
- A combustão ocorre a pressão constante , enquanto o volume aumenta.
- No diagrama, ele aparece como uma linha horizontal de 2 a 3.
Expansão adiabática (3 → 4)
- Os gases queimados se expandem, empurrando o pistão para baixo.
- A pressão diminui à medida que o volume aumenta.
- No diagrama, ele é representado por uma curva descendente de 3 a 4.
Rejeição de calor de volume constante (4 → 1)
- O pistão sobe novamente, expelindo os gases de escape.
- Este processo ocorre em volume constante .
- No diagrama, ele é mostrado como uma linha vertical descendo de 4 a 1.
Desempenho teórico do ciclo diesel
O desempenho teórico do ciclo Diesel é obtido a partir da eficiência térmica , que é expressa em função da taxa de compressão \( r \), da taxa de pressão \( \rho \) e do coeficiente de expansão isentrópica \( \gamma \) (para o ar, aproximadamente 1,4).
Fórmula de desempenho do ciclo diesel
A eficiência térmica do ciclo Diesel é expressa como
\[ \eta_d = 1 - \frac{1}{r^{\gama - 1}} \cdot \frac{\rho^\gama - 1}{\gama (\rho - 1)} \]
onde:
- \( \eta_d \) = eficiência térmica do ciclo Diesel.
- \( r = \frac{V_1}{V_2} \) = taxa de compressão.
- \( \rho = \frac{V_3}{V_2} \) = razão de pressão na combustão.
- \( \gamma \) = coeficiente de expansão isentrópica (para o ar, \( \gamma \approx 1,4 \)).
O desempenho do ciclo Diesel é geralmente inferior ao do ciclo Otto para a mesma taxa de compressão \( r \), mas permite trabalhar com taxas de compressão mais altas, o que melhora sua eficiência na prática.
Análise termodinâmica do ciclo diesel
O ciclo Diesel ideal consiste em quatro processos principais:
- Compressão adiabática (1 → 2).
- Adição de calor a pressão constante (2 → 3).
- Expansão adiabática (3 → 4).
- Rejeição de calor de volume constante (4 → 1).
A eficiência térmica é definida como a razão entre o trabalho líquido \( W_{\text{líquido}} \) e o calor fornecido \(Q_{\text{soma}} \):
\[ \eta_d = 1 - \frac{Q_{\text{rech}}}{Q_{\text{soma}}} \]
Onde:
- \( Q_{\text{sum}} = m c_p (T_3 - T_2) \) é o calor fornecido.
- \( Q_{\text{rech}} = m c_v (T_4 - T_1) \) é o calor rejeitado.
Cálculo do calor fornecido \(Q_{\text{soma}} \)
O calor fornecido ocorre durante o processo 2 → 3 (combustão a pressão constante) e é expresso como:
\[ Q_{\text{soma}} = m c_p (T_3 - T_2) \]
Cálculo do calor rejeitado \(Q_{\text{rech}} \)
O calor rejeitado ocorre no processo 4 → 1 (resfriamento a volume constante):
\[ Q_{\text{rech}} = m c_v (T_4 - T_1) \]
Dividindo ambas as expressões:
\[ \frac{Q_{\text{rech}}}{Q_{\text{soma}}} = \frac{c_v (T_4 - T_1)}{c_p (T_3 - T_2)} \]
Usando a relação entre calores específicos:
\[ \frac{c_v}{c_p} = \frac{1}{\gama} \]
Você obtém:
\[ \eta_d = 1 - \frac{1}{\gama} \cdot \frac{T_4 - T_1}{T_3 - T_2} \]
Expressão baseada na taxa de compressão e na taxa de pressão
Para expressar o desempenho em termos de taxa de compressão \( r \) e taxa de pressão \( \rho \) , usamos as seguintes relações termodinâmicas para processos adiabáticos:
-
Compressão adiabática (1 → 2):
\[ T_2 = T_1 r^{\gama - 1} \] -
Expansão adiabática (3 → 4):
\[ T_4 = T_3 \esquerda(\frac{1}{r}\direita)^{\gama - 1} \]
Além disso, na combustão de pressão constante (2 → 3):
\[ \frac{T_3}{T_2} = \rho\]
Substituindo essas relações na equação de desempenho:
\[ \eta_d = 1 - \frac{1}{r^{\gama - 1}} \cdot \frac{\rho^\gama - 1}{\gama (\rho - 1)} \]
